In diesem Kapitel wird erläutert, wie man ein Neuronales Netz zur Identifikation des doppeltinversen Pendels einsetzen kann. Weiterhin wird gezeigt, wofür man das so trainierte Neuronale Netz benutzen kann.
Wie bereits in Kapitel 
erläutert, schaltet man
parallel zu dem zu identifizierenden System, also dem doppeltinversen
Pendel, das Neuronale Netz, siehe Abbildung . Die
Eingabe an das Netz ist der aktuelle Zustand des Pendelsystems beschrieben
durch Winkel, Geschwindigkeiten, etc., sowie die durch den Regler
ermittelte Kraft. Das Pendelsystem bekommt als Eingabe nur die Kraft, die
Eingabe des Zustandes ist nur fiktiv. Aus dem Unterschied der Ausgaben des
Pendelsystems und des Neuronalen Netzes ist ein Fehlermaß ermittelbar und
hiermit das Neuronale Netz trainierbar.
Abbildung: Identifikation des Pendelsystems.
Zur Identifikation muß man Online, also am laufenden doppeltinversen Pendel, lernen können. Außerdem benötigt man einen Regler, der das Pendel nicht umfallen läßt. Das Echtzeitlernen war am Hardwaremodell nicht möglich. Deswegen wurde ein mathematisches Modell erstellt, siehe Heul96, mit dem das Pendelsystem simuliert wurde. Durch das Verwenden eines Simulationsmodells ist es jedoch notwendig, zu überprüfen, ob das Modell mit dem Hardwaremodell annähernd übereinstimmt. Um das Pendelsystem identifizieren zu können, muß man dessen Reaktion auf einen Regler kennen. Deshalb benötigt man zuerst einen Regler, der das Pendelsystem so regelt, daß es nicht umfällt. Erst dann kann man es identifizieren. Hat man keinen Regler zur Verfügung, kann man dies mit dem Simulationsmodell umgehen. Ersetzt man das Pendel durch das Simulationsmodell, so kann man am Simulationsmodell das doppeltinverse Pendel identifizieren. Der Vorteil dieser Methode ist, daß kein gelernter Regler benötigt wird, der dafür sorgt, daß das Pendel beziehungsweise das Simulationsmodell stehen bleibt. Statt dessen kann man einen ,,Zufallsregler`` benutzen, der zufällig eine Stellgröße ermittelt. Für die Identifikation ist nur die Reaktion des doppeltinversen Pendels auf diese Stellgröße hin notwendig. Am Hardwaremodell ist das nicht möglich, da dieses bei einem Zufallsregler sehr schnell umfällt und jedesmal per Hand aufgerichtet werden muß.
Hat man erst einmal ein Neuronales Netz das System des doppeltinversen
Pendels identifizieren lassen, so kann man dies zur Emulation des
Pendelsystems, siehe Abbildung , benutzen. Dies ist vor
allen Dingen dann notwendig, wenn man das Neuronale Netz zur Regelung des
Systems nicht Online lernen kann. In dem Fall des doppeltinversen Pendels
ist diese Notwendigkeit durch zwei Punkte gegeben. Zum einen ist für das
Lernen des Neuronalen Reglers ein erheblicher Rechenaufwand, je nach
Netzart und -größe, nötig, zum anderen müßte man das Pendel nach
jedem Fehlschlag per Hand wieder aufrichten.
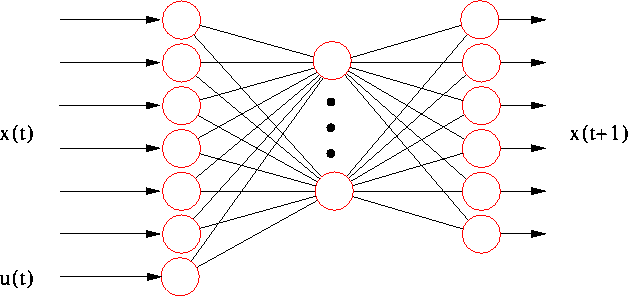
Abbildung: Emulator Netz: Das Netz bekommt als Eingabe den aktuellen
Zustand x(t) und die Kraft u(t) und liefert als Ausgabe den
nächsten Zustand x(t+1). Es ersetzt das doppeltinverse Pendel.
Der Vorteil des Emulatornetzes konnte beim doppeltinversen Pendel nicht genutzt werden. Das Emulatornetz konnte aus oben erwähnten Gründen nur am Simulationsmodell gelernt werden. Auch der Rechenaufwand des Simulationsmodells war geringer als der des Emulatornetzes, so daß nur das Simulationsmodell verwendet wurde.
%