Wie in Kapitel 4.2 schon beschrieben, sind die Ergebnisse
des verwendeteten Algorithmus meist nicht optimal. Dies gilt
eigentlich für alle neuronalen Ansätze,
bei einer Problemstellung dieser Art. Nichtsdestoweniger sind die
gefundenen Weglängen von sehr guter Qualität. In der Praxis wird
i.a. auch nicht die optimale Lösung sondern eine sehr gute Lösung
gebraucht. Diese muß aber in einer vernünftigen Zeit vorliegen, was
viele Verfahren bei großer Anzahl Städte schon ausschließt.
Dieser Algorithmus ist dagegen relativ schnell. Bei 150 Städten ist er
in unter einer Minute fertig. Bei einem Durchlauf mit 1000 Städten
dauert es etwa 15 Minuten. Hierbei ist anzumerken, daß alle
Durchläufe mit 
durchgeführt
wurden. Wie in Kapitel 4.1 beschrieben, kann 
ohne
große Qualitätseinbußen auf 
erhöht werden, was die ganze
Berechnung um den Faktor 10 beschleunigt. Alle Angaben beruhen
auf Meßungen auf einer Sun Sparc 20 (sisyphus).
Im Vergleich zu anderen neuronalen Ansätzen, wie dem von Hopfield
(vgl. [HT86]) sind die Ergebnisse wirklich hervorragend. Vor allem
ist zu betonen, daß dieser Algorithmus immer zulässige Wege findet, wobei
jede Stadt wirklich nur einmal besucht wird. Dies ist z.B. bei dem
Verfahren nach Hopfield ein großes Problem.
Abschließend kann man sagen, daß dieser Algorithmus eine sehr brauchbare
Lösung für das Problem des Handlungsreisenden liefert. Natürlich
gibt es noch bessere bzw. schnellere Verfahren, auch aus dem
Neuronalen Bereich.
Dafür ist der hier gewählte Ansatz relativ einfach, sowohl in
der Implementation, als auch im Verständnis.
Figure: Beispiel für einen Durchlauf mit 50 Städten
Figure: Beispiel für die Funktionsweise mit 50 Städten
Figure: Beispiel für Schleifen bei 150 Städten
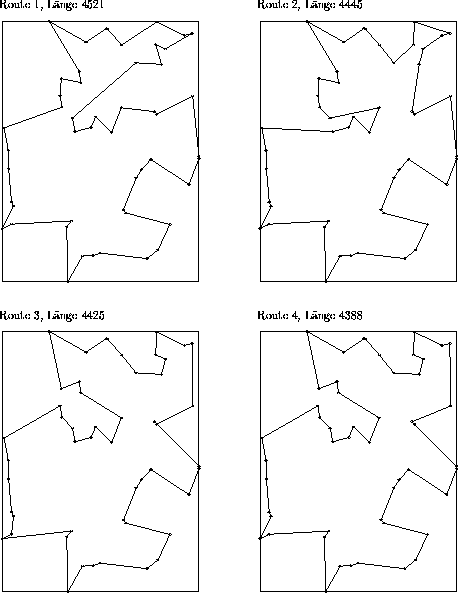
Figure: Beispiel für verschiedene Routen bei gleichem Stadtplan, 50 Städte
